2.2-Teorema de Fourier
¿Qué dice?
Observemos una función periódica
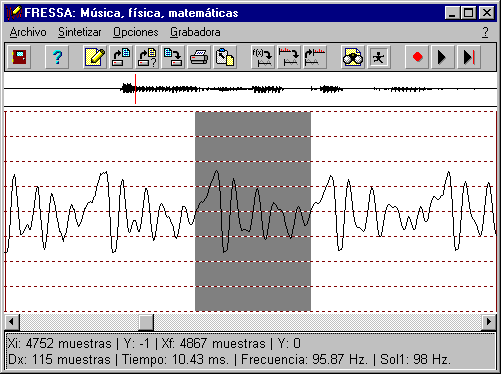
Para hacer todos las integrales y el cálculo de las funciones series de Fourier lo hacemos a través del programa FRESSA.
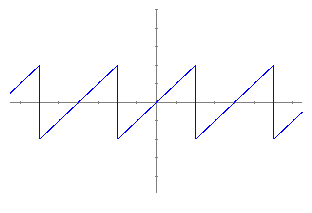
Observemos una función periódica
Esta función se llama diente de sierra.
El teorema de Fourier dice que dada una función periódica esta puede ser aproximada mediante la serie de Fourier, con mejor aproximación cuanto más términos cojamos.
Dada una función F(x) la serie de Fourier es la siguiente función:
donde an y bn son los llamados coeficientes de Fourier de la función F(x) y se calculan mediante las siguientes fórmulas:
y
Donde 2l es el valor del período. En el ejemplo 4 · n = 0,1,2,3,4,...
La justificación de estas fórmulas esta fuera del alcance del nivel al cual dirigimos este trabajo, pero lo que representan, si. Veamos qué representa el Teorema de Fourier. En primer lugar vamos a calcular los diferentes coeficientes de la serie, para ello debemos calcular las integrales definidas:
Nuestra función periódica es impar. Se puede demostrar que las funciones impares todos los valen 0. En las pares son los que siempre valen 0.
Si calculamos b1 = 1´273076
Y representamos la función periódica junto con:
que es el primer término de la serie de Fourier, observamos lo siguiente:
Si calculamos b2 = -0´636292
Y representamos la función periódica junto con:
que son los dos primeros términos de la serie de Fourier, observamos lo siguiente:
Si continuamos y calculamos hasta el quinto término
g(x)=1.273076 sen(px/2) -0.636292 sen(2px/2) +0.423922 sen(3px/2)
-0.317655 sen(4px/2) +0.253829 sen(5px/2)
y si representamos las dos gráficas, observamos:
Si calculásemos más términos veríamos que podemos construir la función periódica con tanta aproximación como deseemos mediante la suma de funciones trigonométricas de frecuencia 1, 2, 3, 4, 5, 6... veces la fundamental
Recordemos que una función
tiene de período T y frecuencia 1/T . O sea nuestras funciones tienen frecuencias 1/4, 2/4, 3/4, 4/4, 5/4,...
Eso hace que un La emitido por una guitarra y que decimos que vibra a una frecuencia de 440 Hz. y vemos que su oscilograma no tiene una forma senoidal pura, en realidad sea la suma de distintas funciones senoidales de frecuencias 440, 880, 1320, 1760, 2200,... Hz. multiplicados por unos coeficientes que podemos conocer si calculamos los coeficientes de la serie de Fourier.
Podemos agradecer al señor Fourier que nos ofreció un método para descomponer los sonidos de los instrumentos musicales en sus distintos componentes de frecuencia.
Parece ser que nuestro oído cuando escucha los sonidos realiza naturalmente esta descomposición y así nuestro cerebro puede percibir y distinguirlos.
La diferencia de sonido de diferentes instrumentos musicales tocando una misma nota, llamada timbre, podemos, en primera aproximación, decir que es debida a las distintas composiciones de los componentes de Fourier. Coeficientes de Fourier distintos para cada instrumento.
La conclusión interesante que podemos deducir de todo esto, es que podemos analizar los sonidos mediante el cálculo de los coeficientes de Fourier y saber que cantidad de armónicos tienen los timbres de distintos instrumentos. Y al revés, calculando las funciones series de Fourier podemos sintetizar sonidos. En la práctica veremos las limitaciones de esto, Estudio de un timbre. La guitarra. Análisis y síntesis de sonidos.
Para hacer todos las integrales y el cálculo de las funciones series de Fourier lo hacemos a través del programa FRESSA.
BIBLIOGRAFÍA
Para conocer mejor las series de Fourier recomendamos trabajar con:
Funciones para Windows. MEC. 1993.





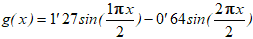





Comentaris
Publica un comentari a l'entrada